Theory

In a linear time invariant network when the resistance `(R)` of an uncoupled branch, carrying current (I), is changed by ΔR_L , the currents in all the branches would change and can be obtained by assuming that an ideal voltage source of V_c has been connected such that V_c=IΔR_L in series with R+ΔR_L when all other sources in the network are replaced by their internal resistances.

Explanation :  

Let us assume a load `R_L` connected to a dc source network whose thevenin's equivalent gives V_o as the Thevenin's voltage and R_Th as Thevenin resistance.

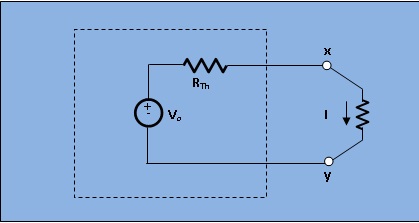
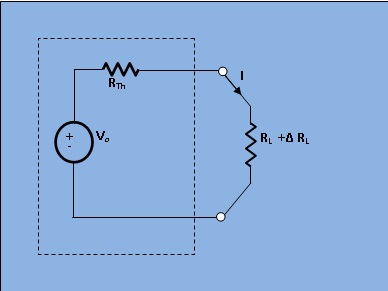
Let the load resistance R_l be changed to R+ΔR_L.Since the rest of the circuit remains unchanged,the Thevenin equivalent network remains the same.This Change of current being termed as ΔI , we find

$$\Delta I = I' - I$$

     $$= \frac{V_o}{(R_{Th} + R_L + \Delta R_L)} - \frac{V_o}{(R_{Th} + R_L)}$$

     $$= \frac{V_o (-\Delta R_L)}{(R_{Th} + R_L)(R_{Th} + R_L + \Delta R_L)}$$

     $$= -\frac{V_c}{R_{Th} + R_L + \Delta R_L} .......(3)$$

$$V_c = I \Delta R_L$$

This voltage V_c is termed as compensating voltage.